The Forward Pass

In this post we will begin implementing our neural net. We will start by implementing the basic data structures that comprise our neural net. Then I explain what exactly happens during the forward pass, followed by the code.

The Neural Net Class

First thing’s first we need a neural net:

import numpy as np
import random

class Net:
    def __init__(self, sizes):
        self.layers = [Layer(sizes[x + 1], sizes[x]) for x in range(len(sizes) - 1)]

Each layer in our net will need 2 sizes to be initialized:

The number of neurons in the layer
The number of neurons in the previous layer

It is important to note that the input layer does not actually have a layer object associated with it. As I described in the previous post, the input layer does not actually have neurons. It is the input to our net. We still need to take its size into account, however, because there are still weights connecting the input layer to the first hidden layer.

What Happens in the Forward Pass?

I have broken up the code for the forward pass into two functions. The first is not that interesting. It just iterates over the layers, passing the output of the previous layer into the new layer to produce the new output and so on until there are no more layers at which point we return the final output.

class Net:
    def __init__(self, sizes):
        self.layers = [Layer(sizes[x + 1], sizes[x]) for x in range(len(sizes) - 1)]
    
    def forward(self, inputs):
        current_a = inputs
        for layer in self.layers:
            a = layer.feed_forward(current_a)
            current_a = a
        return current_a

The feed_forward method is where the real work happens.

For each layer we take the output of the previous layer and use it for our input. For each neuron in the layer we multiply it by the weights, add the biases, then pass that weighted sum to the activation function.

Imagine we have 2 inputs and 1 neuron in the hidden layer:

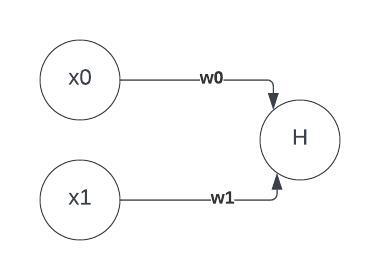
We would take the 2 inputs, $x_0$ and $x_1$ , and multiply them by their corresponding weights, $w_0$ , and $w_1$ . We would sum these products together, and add the bias. We would then pass all of that into the activation function.

$\sigma(\sum_nx_nw_n + b)$

Note that I am denoting the activation function with a $\sigma$ . The sigmoid function is a widely used activation function, but this could be any activation function. We will be using sigmoid in our implementation.

Here is the code for the sigmoid function:

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

In practice, for both efficiency and simplicity, we will use matrix multiplication to represent $\sum_nx_nw_n$ .

This means that we can represent the weighted sum of the neuron, $z$ with this equation:

$z = w \cdot x + b$

Each layer in our net will have a weight matrix, $w$ . The weight matrix will have $n$ rows, where $n$ is the number of neurons in the layer, and $m$ columns, where $m$ is the number of neurons in the previous layer. The entries in this matrix represent all of the weights connecting the previous layer to the current layer.

In our simple example of 2 input neurons and 1 hidden layer neuron, our weight matrix for the hidden layer would look like this:

$\begin{bmatrix} w_0 & w_1 \end{bmatrix}$

Or, for a more interesting example, let’s say we had 4 input neurons and 3 hidden layer neurons. Then $w$ would be:

$w = \begin{bmatrix} w_{11} & w_{12} & w_{13} & w_{14}\\ w_{21} & w_{22} & w_{23} & w_{24} \\ w_{31} & w_{32} & w_{33} & w_{34}\\\end{bmatrix}$

We will also represent the biases as a vector. Each entry in the vector represents the bias for a neuron in the layer.

So the feedforward method will need to do three things:

Compute the weighted sum, $z$ , using the equation: $z = w \cdot x + b$ .
Compute the activation values by passing the weighted sums into the sigmoid function.
Return the activation values.

The Layer Class

Now that we know what kind of data our layer will need we can implement the Layer class. I have also put the feedforward method in this class:

class Layer:
    def __init__(self, size, n_inputs):
        self.weight_matrix = np.random.randn(size, n_inputs)
        self.biases = np.random.randn(size, 1)

    def feed_forward(self, input):
        weighted_sums = np.dot(self.weight_matrix, input) + self.biases
        activations = sigmoid(weighted_sums)
        return activations

Conclusion

This is all we need to pass input into our neural net, and get out an output. Here is what the code for that would look like:

x = [2.0, 3.0, -1.0]
x = np.reshape(x, (3, 1))

net = Net([3, 3, 1])

output = net.forward(x)

It is important to note that our neural net is expecting a column vector as its input, which is why we need to call numpy.reshape().

In the next blog post I will go over how to train this neural net so that we can get it to output the values we are expecting, and even produce the correct output for values outside its training set.