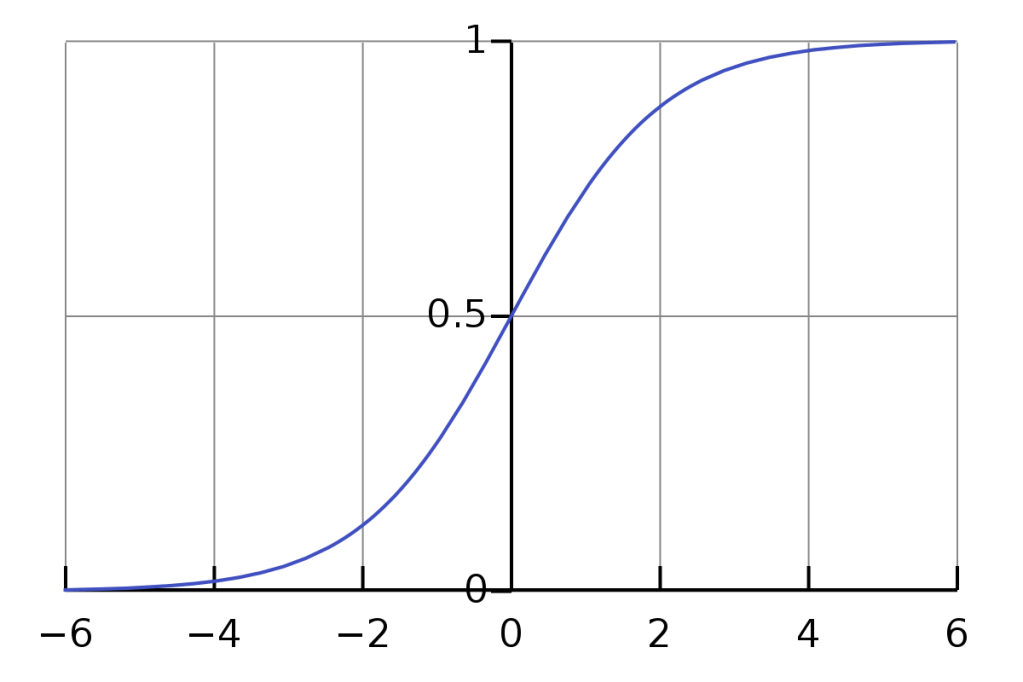
The Derivative of the Sigmoid Function

,
, , , ,

The sigmoid function, \sigma is a popular activation function for neurons in a neural net.

It is necessary to use the derivative of the activation function when using backpropagation to compute the gradients of the weights and biases of the network.

Here is how to find the derivative of the sigmoid function:

Let’s take a look at the equation for the sigmoid function:

\sigma = \dfrac{1}{1 + e^{-z}}

To begin, let’s rewrite this fraction as a negative exponent:

\sigma = (1 + e^{-z})^{-1}

Now we can apply the chain rule:

The “inner function” is:

g(z) = 1 + e^{-z}

The “outer function” is:

f(z) = z^{-1}

So, first we find the derivative of the “inner function”:

g'(z) = -e^{-z}

Now we find the derivative of the “outer function” if the “inner function” were just a variable:

f'(z) = -(1 + e^{-z})^{-2}

Now, as per the chain rule, we multiply them together:

\sigma'(z) = g'z * f'(z)

\sigma'(z) = -e^{-z} * -(1 + e^{-z})^{-2}

Let’s convert our negative exponent back to a fraction:

\sigma'(z) = \dfrac{e^{-z}}{(1 + e^{-z})^2}

Let’s factor this into two pieces:

\sigma'(z) = \dfrac{1}{1 + e^{-z}} \cdot \dfrac{e^{-z}}{1 + e^{-z}}

We can rewrite the numerator of the second part to look like this:

\sigma'(z) = \dfrac{1}{1 + e^{-z}} \cdot \dfrac{(1 + e^{-z}) - 1}{1 + e^{-z}}

All we did was just add 1 to the numerator and then subtract 1. This does not change the value at all, but it allows us to factor like this:

\sigma'(z) = \dfrac{1}{1 + e^{-z}} \cdot \dfrac{1 + e^{-z}}{1 + e^{-z}} - \dfrac{1}{1 + e^{-z}}

Simplifying further gives us:

\sigma'(z) = \dfrac{1}{1 + e^{-z}} \cdot 1 - \dfrac{1}{1 + e^{-z}}

We know that: \sigma(z) = \dfrac{1}{1 + e^{-z}}, so we can substitute into our equation which finally gives us:

\sigma'(z) = \sigma(z) \cdot (1 - \sigma(z))

One response to “The Derivative of the Sigmoid Function”

  1. The Cross-Entropy Loss Function – Robert Vagene's Blog

    […] We know that the derivative of the sigmoid function is equal to (see The Derivative of the Sigmoid Function): […]

    Like

    Reply

Leave a reply to The Cross-Entropy Loss Function – Robert Vagene's Blog Cancel reply